期權的風險指標通常用希臘字母來表示，包括：delta值、gamma值、theta值、vega值、rho值等
Delta值（δ），又稱對沖值：是衡量標的資產價格變動時，期權價格的變化幅度 。用公式表示：Delta=期權價格變化/期貨價格變化
所謂Delta，是用以衡量選擇權標的資產變動時，選擇權價格改變的百分比，也就是選擇權的標的價值發生變動時，選擇權價值相應也在變動。
公式為：Delta＝外匯期權費的變化／外匯期權標的即期匯率的變化
關于Delta值，可以參考以下三個公式:
1.選擇權Delta加權部位＝選擇權標的資產市場價值×選擇權之Delta值;
2.選擇權Delta加權部位×各標的之市場風險系數＝Delta風險約當金額;
3.Delta加權部位價值＝選擇權Delta加權部位價值＋現貨避險部位價值。
Delta具有以下特性：買權的Delta一定要是正值； 賣權的Delta一定要是負值; Delta數值的范圍介乎0到1之間; 價平選擇權的Delta為0.5; Delta數值可以相加，假設投資組合內兩個選擇權的Delta數值分別為0.5及0.3，整個組合的Delta數值將會是0.8。
對于看漲期權來說，期貨價格上漲（下跌），期權價格隨之上漲（下跌），二者始終保持同向變化。因此看漲期權的delta為正數。而看跌期權價格的變化與期貨價格相反，因此，看跌期權的delta為負數。
風險指標的正負號均是從買入期權的角度來考慮的。因此，交易者一定要注意期權的指標與部位的指標之區別。對于delta，期權部位的符號如下表。
表1期權部位的delta值
| 部位 | 看漲期權 | 看跌期權 |
|---|---|---|
| 多頭 | + | - |
| 空頭 | - | + |
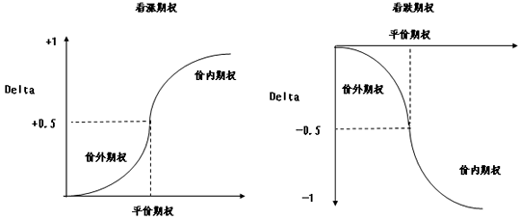
期權的delta值介于-1到1之間。對于看漲期權，delta的變動范圍為0到1，深實值看漲期權的delta趨增至1，平值看漲期權delta為 0.5，深虛值看漲期權的delta則逼近于0。對于看跌期權，delta變動范圍為-1到0, 深實值看跌期權的delta趨近-1，平值看跌期權的 delta為-0.5，深虛值看跌期權的delta趨近于0。期貨的Delta為1。
δ的取值范圍在-1到+1之間，它與期權內在價值的關系如下表：
| δ值 | |||
|---|---|---|---|
| 價內期權 | 平價期權 | 價外期權 | |
| 看漲期權 | 0 < δ < +0.5 | δ = +0.5 | +0.5 < δ < 1 |
| 看跌期權 | -0.5 < δ < 0 | δ = -0.5 | -1< δ < -0.5 |
舉例而言，某投資者考慮買入執行價格為1.2800，面值為100歐元的歐元美元看漲期權合約。現在市場歐元美元匯率為1.2800，該外匯期權的值為+0.5。這就是說，如果市場歐元美元匯率漲至1.2900－－上漲0.01美元，那么該期權價格將上漲+0.5×0.01×100＝0.5美元。
價外程度很深的外匯期權很小，接近于0。這就是說市場即期匯率的變動對期權價格的影響很小，或者說期權價格幾乎不受市場匯率變化的影響。相反，價內程度很深的外匯期權很大，接近于±1。也就是說，任何即期匯率的變動將導致期權價格差不多同等幅度的變動，這導致投資者所面臨的風險與持有等額標的資產的風險一模一樣。如下圖：
需要注意的是，外匯期權的Delta并不是一個靜態概念，它將隨著到期時限、即期匯率水平以及期權價格水平的不同而隨時發生變化。這就意味著，只有在即期匯率發生微小變化時，Delta預測的結果才是有效的。
權證的Delta值總是介于0與100%之間。價平權證的Delta值在50%區域附近，越是價內的權證其Delta值越是接近100%，越是價外的權證其Delta值越是接近0。這里的價平指行權價和標的證券的現價一樣，價內和價外分別指行權價小于現價和行權價大于現價。Delta值的大小反映了權證到期成為價內的概率，價平的權證其到期時成為價內的權證的可能性接近50%，深度價內的權證到期時成為價內的權證的可能性接近100%，而深度價外的權證其到期時成為價內的可能性幾乎為0。
簡單來說，對于給定的行權價格，如果標的證券的價格越低，其Delta越小，如果價格很低，Delta就會接近于0；隨著價格的上升，Delta就變大，當價格很高了，其Delta就會接近于1，意味著在權證到期時投資者肯定能得到一定的收益。
1、衡量部位風險。如看漲期權的delta為0.4，意味著期貨價格每變動一元，期權的價格則變動0.4元。Delta具有可加性，如果投資者持有以下投資組合：
表2 投資組合的delta值
| 持倉部位 | Delta | 數量（張） |
| 買入小麥期貨 | 1 | 1 |
| 買入看漲期權 | 0.47 | 2 |
| 買入看跌期權 | -0.53 | 3 |
總體持倉部位風險狀況如何呢？可以將所有部位的Delta值相加：1+2×0.47-3×0.53=0.35
可見，該交易者的總體持倉的Delta值為0.35，也就是說這是一個偏多的部位，相當于0.35手期貨多頭。
2、 Delta中性套期保值（Delta Hedging）。如果投資者希望對沖期權或期貨部位的風險,Delta就是套期保值比率。只要使部位的整體 Delta值保持為0.就建立了一個中性的套期策略。例如，投資者持有10手看跌期權，每手看跌期權的Delta值為-0.2，部位的Delta為-2. 投資者可以采取以下任何一種交易，均可以實現部位Delta的中性，規避10手看跌期權多頭的風險。
